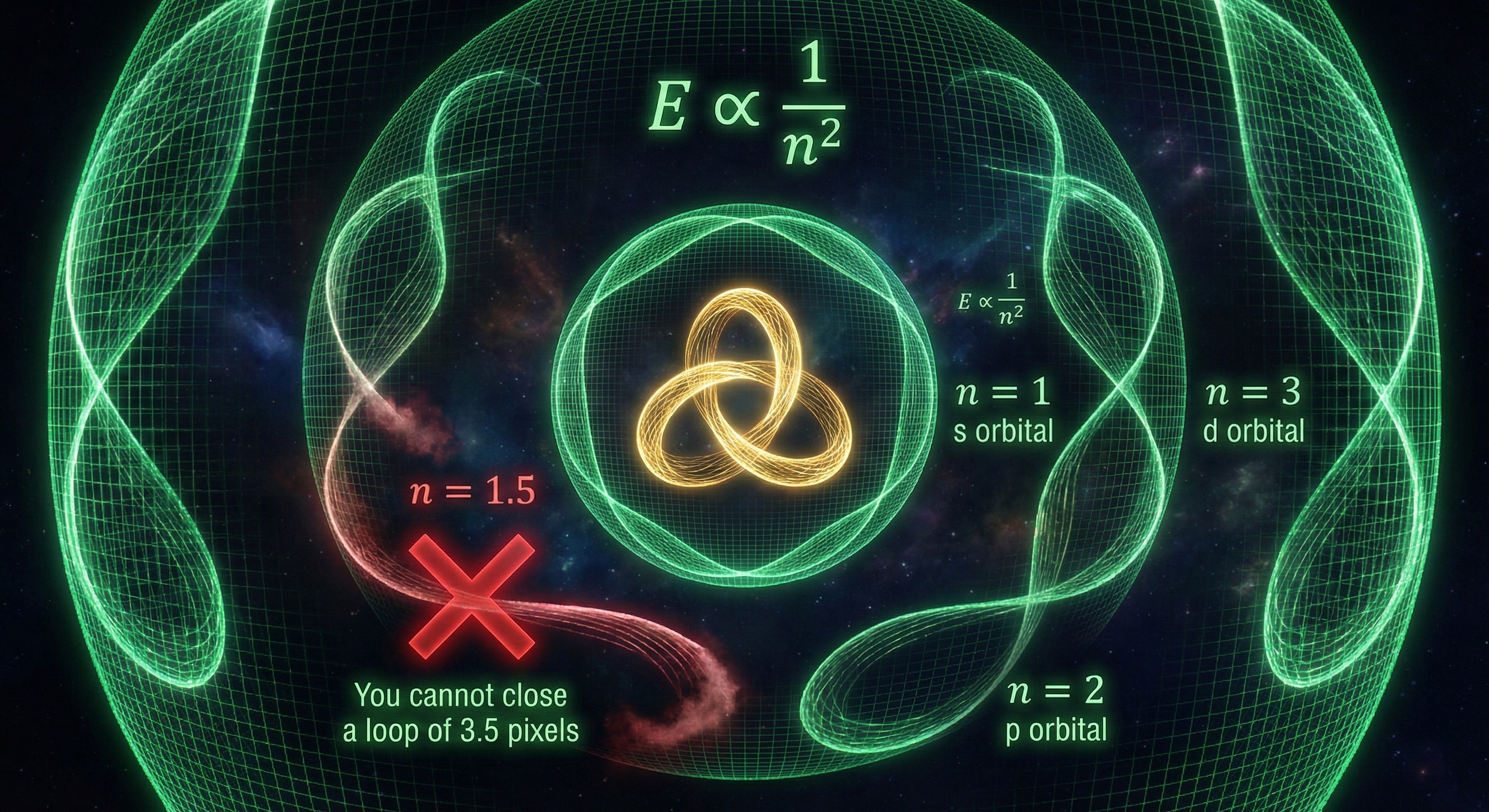"You cannot close a loop of 3.5 pixels on a graph. It must be an integer."
Abstract
In standard physics, we say the electron is a wave, and an orbit must contain an integer number of wavelengths ($2\pi R = n\lambda$). In the Voxel Graph model, this is much more literal. Space is not continuous — it is a lattice. The electron is a cyclic pattern (a twist) moving on this lattice. Quantization is simply the loop closure condition on the graph.
I. Why Everything is Quantized
In the Graph Universe, space is not continuous. It is a lattice.
The electron is a cyclic pattern — a twist — that propagates on this lattice.
For an "orbit" to be stable, the path must bite its own tail exactly.
On a discrete network, if you complete a cycle and land "between two nodes," the pattern breaks (destructive interference / decoherence). The network cannot sustain this vibration.
Quantization is the loop closure condition on the graph.
Either the cycle makes exactly $n$ jumps to return to its starting point (phase 0), or it does not exist. There is no orbit "1.5".
On a pixel grid, you cannot draw a circle with a non-integer circumference.
The circle either closes perfectly, or it doesn't close at all.
II. The Mechanism: The Electron "Tiles" the Proton's Sphere
How do we find the energy levels?
Recall that the Proton is a Topological Knot ($T^5$) that creates tension (gravity/electric) in the network.
The Electron (negative) is the network's response trying to cancel this tension. It tries to "hide" the proton by wrapping around it.
Imagine the Proton is a ball. The Electron is a fabric you're trying to wrap around it.
Problem: You cannot perfectly wrap a sphere with a flat plane (the map projection problem).
Solution: You must create Folds or Harmonics.
The "Orbitals" ($s, p, d, f$) are the different geometric ways to tile the sphere surrounding the proton with the electron's pattern.
Each orbital type represents a different solution to the sphere-tiling problem — a different way to create a closed, self-consistent pattern on the holographic surface surrounding the proton.
III. Derivation of the $1/n^2$ Levels
Let's derive the famous Rydberg formula $E_n \propto -1/n^2$ from the network.
A. The Geometry of the Void (Recall Post 024)
We proved that the network tension (the potential $V$) around the proton decays as $1/R$ due to holographic projection on the sphere $4\pi R^2$.
B. Quantization of Action (The Twist)
The electron is a unit twist (Mobius). Its Action $S$ over a closed orbit must be an integer multiple of the network's action unit ($h$).
Where $p$ is the local momentum/tension and $r$ is the path.
C. Energy as Tiling Density
This is where the Graph theory shines.
Energy $E$ of a level is not a "velocity." It is the Twist Density of the network.
If the orbit is wide (large $n$), the electron's twist is "spread" over a much larger surface. Local tension is weaker.
Orbit surface (holographic sphere): $A \propto R^2$
To satisfy the closure condition on a $1/R$ potential, the orbit radius must grow as the square of the node count:
(This is a standard property of central networks: to double the number of waves in a $1/R$ well, you must quadruple the distance.)
Energy Density: Energy is the inverse of the topological container's size (smaller = more tension).
The levels $n=1, 2, 3...$ are the only holographic spheres whose pixel surface ($R^2$) allows drawing a closed pattern of length $n$ without seam errors.
IV. The Link to $6\pi^5$ (Fine Structure)
Can we go beyond Bohr? Yes.
The standard model struggles to explain why the ground state is stable — why the electron doesn't crash into the proton.
The Graph theory explains this through the Topological Exclusion Volume.
The Proton is not a point. It is a $T^5$ volume of size $6\pi^5$.
The level $n=1$ (ground state) is the minimal sphere that can contain this topological volume without penetrating it.
The electron cannot descend further ($n=0$) because it would collide with the rigid structure of the $T^5$ knot. There is a Topological Barrier.
This suggests that the exact value of the ground state energy (13.6 eV) is directly calculable from the ratio between the electron's Twist tension and the Proton's volume $6\pi^5$.
V. Summary: The Atom as Graph Resonance
The Hydrogen Atom in Graph Theory
- Why quantized? Because you cannot close a loop of 3.5 pixels on a graph. It must be an integer.
- Why stable? Because the proton is a solid ($6\pi^5$) that prevents collapse.
- Why $1/n^2$? It's the dilution law of a twist's tension on a holographic spherical surface.
Standard Physics
"The electron is a wave"
"Orbits must have integer wavelengths"
"Quantization is mysterious"
Graph Theory
"The electron is a twist on a lattice"
"Loops must close exactly"
"Quantization is geometry"
The atom is not a miniature solar system. It is not a probability cloud. It is a Graph Resonance — a standing wave pattern that exists because, and only because, it closes perfectly on itself. The universe doesn't allow half-pixels.